Variational Inference 관련 내용 정리

Variational Inference는 확률을 추론하는 문제를 위한 알고리즘이다. 확률 계산이 불가능한 상황에서 임의의 확률분포를 도입하고 최적화 문제로 바꾸어서 근사적인 방법으로 문제를 푼다. 

Variational Inference를 알기 위해서는 다음과 같은 지식들을 알면 좋다. 

• Probabilistic Graphical Model
• Probabilistic Inference
• Bayesian Inference

 

 

1. Probabilistic Graphical Model

그림1: Probabilistic Graphical Model

  랜덤변수들의 집합이 있다고 할 때, 그 랜덤변수들 간의 의존성(dependency)를 보기 쉽게 그래프로 표현한 것을 확률적 그래프 모델(Probabilistic Graphical Model)이라고 한다. PGM의 종류로는 세 가지가 있다. 

• Bayesian Network
• Markov Network
• Factor Graph

 

  베이지안 네트워크의 경우 비순환 방향성 그래프로 표현되며 랜덤변수 간의 의존성이 (조건부) 그림 1의 왼쪽처럼 화살표로 표시된다. 만약 랜덤변수들의 결합분포를 구하고자 한다면 $p(X, Y, Z) = p(Z|X, Y)p(Y|X)p(X)$를 계산해야 하지만 조건부 독립을 이용하면 $p(X, Y, Z) = p(Z|X)p(Y|X)p(X)$를 계산하면 된다.

  마르코프 네트워크의 경우 방향성 그래프로 표현되며 변수들 간의 의존성이 일직선으로 표현된다. 팩터 그래프의 경우는 그래프에서 몇몇 변수의 함수들을 factorization을 통해 표현한 것이다. 

 

 

2. Probabilistic Inference

  통계학에서 배우는 통계적 추론(Statistical Inference)은 모집단에 대한 어떤 양상을 알기 위해 모수추정(parameter estimation) 또는 가설검정(testing hypothesis)를 수행한다. 그러면 확률적인 추론(Probabilistic Inference)란 무엇일까? 위키피디아에서는 확률적 추론이 통계적 추론의 한 방법이라고 말하고 있다. Daphne Koller의 Probabilistic Graphical Models 책에서는 확률추론 문제를 다음과 같이 정의한다. 

 Probabilistic inference is a type of statistical inference. "Probabilistic inference" was introduced and roughly defined in the PGM context as any marginalisation task of a probability function, whether it is a marginal probability computation or finding the most probable outcome (for e.g. classification)

즉, 설명하자면, 베이지안 네트워크나 마르코프 네트워크 같은 어떤 확률 그래프 모형(PGM)에서 확률함수의 주변화(marginalisation)를 수행하는 것으로, 이 과정에서 주변확률이나 조건부확률을 계산하는 문제를 푸는 것이다.

 

3. Bayesian Inference

  베이즈 추론은 추론해야 하는 대상의 사전확률(prior)과 데이터를 기반으로 계산한 가능도(liklihood)를 통해 대상의 사후확률(posterior)를 계산하는 방법이다. 베이즈룰은 다음과 같다. 

$$ P(\theta | X) = {P(X|\theta)P(\theta) \over P(X)} $$

$$ P(X) = \sum_{x \in X} p(x|\theta )P(\theta) \ \text {or} \ \int p(x|\theta )P(\theta)dx $$

  머신러닝의 관점에서 회귀문제나 분류 문제를 푸는 모델을 생각해보자. 현재 대세적인 방법은 liklihood $P(X|\theta)$를 최대화하기 위해 고정된 데이터셋 $X$에 대한 예측값을 출력하고 손실함수를 계산하여 gradient descent로 최적의 파라미터를 향해 업데이트 한다.

  위 식의 베이즈 룰을 사용하면 데이터가 추가로 들어올 때마다 베이지안 방식으로 모델 파라미터를 업데이트 할 수 있다. 베이지안 방식으로 파라미터를 업데이트 하면 오버피팅을 방지 할 수 있고 노이즈에 더욱 강건하다고 한다 (PRML ch4). 이렇게 사전확률과 추가적인 관측 데이터로 베이즈 룰을 통해 사후확률을 계산하는 방법을  Bayesian Inference라고 한다. 하지만 단점으로는 사전확률을 어떻게 정할 것인지의 문제가 있다. 또한 베이즈룰의 오른쪽 우변의 분모를 Evidence라고 하는데 evidence를 계산하기 위해 고차원의 적분, 합 연산을 하는 것이 까다로우며 확률분포를 모르는 경우 이를 계산할 수가 없다! 그래서 근사적인 방법으로 계산하거나 샘플링을 하게 되는데 이 방법들이 라플라스 근사, 몬테카를로 마르코프 체인, 변분추론(Variational Inference)이다. 

 

 

4. ELBO

  베이지안 추론을 할 때, 라플라스 근사 경우 연속형 랜덤변수를 사용해야 하고 특정 위치의 확률밀도함수 값을 가우시안분포로 근사하기에 사용하기에 제약이 많다. [5] 몬테카를로 마르코프 체인 (MCMC) 방법으로 샘플링을 통해 분모를 계산해서 업데이트 하는 방식은 정말로 느리다. [4] 그래서 베이지안 추론 문제를 최적화를 통해서 해결하는 Variational Inference를 많이 사용한다. 변분추론을 이해하기 위해서는 evidence lower bound(ELBO)을 먼저 이해해야 한다.

 

ELBO

 

  evidence lower bound는 어떤 관측값으로 계산된 log-likelihood의 하한이다. 여기서 evidence는 베이즈 룰에서 우변의 분모에 해당했었다.  확률적 추론을 위해 수행하는 알고리즘 (기댓값 최대화, 변분 추론)에서 계산에 매우 유용하다. 이제 어떤 잠재변수를 가진 모델의 확률추론 문제를 풀고 싶다고 생각해보자. 데이터의 경우 랜덤변수 $X$의 관측값(realization)이고 잠재변수는 랜덤변수 $Z$의 확률 분포를 따른다고 하자. 그러면 latent variable model은 $P(X, Z;\theta)$ 라는 결합분포로 표현될 수 있다. 우리는 랜덤변수 $X$ 만 관측할 수 있고, $Z$는 관측할 수 없다. 보통 우리가 풀고 싶은 문제는 다음과 같다. 

 

(1) 주어진 파라미터 $\theta$에 대해서 사후확률분포 $P(Z|X;\theta)$를 계산하는 문제

(2) 파라미터 $\theta$를 알 수 없을 때, 주어진 sample $x$에 대한 $\theta$의 최대우도추정치를 찾고 싶을 때
$$ \arg \max_{\theta} l(\theta), \\ \text {where} l(\theta) := \log p(x;\theta) = \log \int_z p(x, z;\theta)dz$$

 

(1)번 문제를 해결하기 위해 Variational Inference를 사용하게 된다. (2)번 문제를 해결하기 위해서 maximization 사용한다. 둘 다 알고리즘에서 ELBO를 활용한다.

 

ELBO 유도

 

  evidence는 다음과 같이 정의된다. 

$$ \text {evidence} := \log p(x;\theta) $$

  evidence라는 이름이 붙은 이유는 모델 $p$의 파라미터 $\theta$를 잘 선택했을 때, $x$에 대한 주변확률이 커지게 된다. 따라서, 높은 $\log p(x;\theta)$는 우리가 데이터에 대한 좋은 모델을 선택했다는 증거라는 말인 것 같다. 

  이제 식을 유도해보자. 우리는 유도를 위해 전확률 법칙과 젠슨의 부등식을 사용할 것이다. 

$$ \begin{align} \log p(x;\theta) &= \log \int p(x, z;\theta) dz \\ &= \log \int p(x, z;\theta) {q(z) \over q(z) } dz \\ &= \log \mathbb E_{Z \sim q(Z)} \bigg [ {p(x, Z) \over q(Z) }\bigg ]  \\ &\ge \mathbb E_{Z \sim q(Z)} \bigg [ \log {p(x, Z) \over q(Z) } \bigg ] \end{align} $$

유도과정에서 $z$에 대한 임의의 확률분포 $q$를 도입해서 $Z$에 대한 기댓값으로 식을 바꾸었다. 이렇게 하는 이유는 첫 번째 줄의 적분값을 계산할 수 없어서 중요도 샘플링(importance sampling)을 통해 적분값을 계산하는 몬테카를로 적분을 하기 위함이다.   이후 젠슨의 부등식을 통해 lower bound를 유도한다. 수식을 간략히 하기 위해 $\theta$는 생략했다. 따라서 ELBO는 evidence 하한으로써 다음과 같이 정의된다. $$ \text {ELBO} :=  \mathbb E_{Z \sim q(Z)} \bigg [ \log {p(x, Z) \over q(Z) } \bigg ] $$

 

ELBO와 Evidence 사이의 gap

 

부등식을 보아하니 ELBO의 값은 Evidence보다 작다. 그렇다면 얼마만큼 작을까? 유도해보자. $\theta$는 생략한다. 

$$\begin {align} \text {evidence} - \text {ELBO} &= \log p(x) - \mathbb E_{Z \sim q(Z)} \bigg [ \log {p(x, Z) \over q(Z) } \bigg ] \\ &=  \mathbb E_{Z \sim q(Z)} [\log p(x)] - \mathbb E_{Z \sim q(Z)} \bigg [ \log {p(x, Z) \over q(Z) } \bigg ] \\ &= \mathbb E_{Z \sim q(Z)} [\log p(x)] - \mathbb E_{Z \sim q(Z)} [\log p(x, Z)] + \mathbb E_{Z \sim q(Z)} [\log q(Z)]\\ &= \mathbb E_{Z \sim q(Z)} \bigg [- \log{ p(x, Z) \over p(x)} \bigg] + \mathbb E_{Z \sim q(Z)} [\log q(Z)] \\ &= \mathbb E_{Z \sim q(Z)} [-\log p(Z|x)] + \mathbb E_{Z \sim q(Z)} [\log q(Z)] \\ &= \mathbb E_{Z \sim q(Z)} \bigg [\log{ q( Z) \over p(Z|x)} \bigg] \\ &= KL( q(z) || p(z|x)) \end {align}$$

 결과적으로 ELBO와 Evidence 값의 차이는 $q(z)$와 $p(z|x)$의 KL 다이버전스가 된다. 시각화하면 다음과 같다. [8]

 

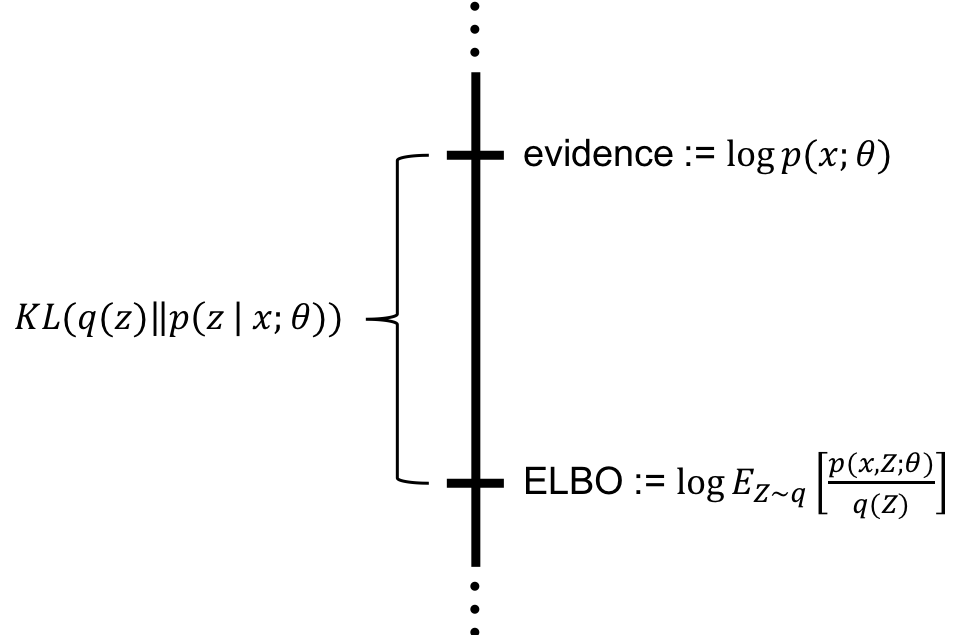
  만약 KL 다이버전스의 값이 0에 가까워 진다면 어떻게 될까? 우리는 임의의 분포 $q(z)$가 $p(z|x)$를 잘 근사했다고 생각할 수 있다! evidence의 lower bound를 찾는 과정에서 근사적인 방법에 대한 실마리를 얻은 것이다. Variational Inference에서는 KL 값을 줄이도록 모델을 최적화하게 된다. 

 

 

5. Variational Inference

Motivation

 

  Variational Inference는 사후확률을 추정하는 high-level 패러다임이다. 특히, 사후확률계산이 불가능할 때 사용된다. 모델에 잠재변수 $Z$가 포함되고, 관측 데이터 $X$가 포함된다면 모델을 확률분포 $P(Z, X)$로 표현할 수 있다.  목적이 사후확률분포 $P(Z|X)$를 계산해야할 때 VI를 사용한다. 만약 사전확률, 가능도, 증거를 모두 알고 있다면 사후확률은 다음과 같이 베이즈 룰을 통해 계산될 수 있다. 

$$ p(z|x) = {p(x|z)p(z) \over p(x)} $$

그러나 실제 문제에서는 사전확률분포도 알려져 있지 않고 evidence를 계산하기 위해서는 $p(x) = \int p(x, z) dz$를 계산해야 한다. 이때, 사후확률을 계산하기 위해서 문제를 최적화 문제로 바꾸어서 근사적으로 사용하는 방법이 Variational Inference다. 

  $p(z | x)$를 베이즈 룰을 통해 정확히 계산하는 것 대신에, VI는 $p(z|x)$와 '가까운' 어떤 임의의 분포 $q(z)$를 찾는다.$q(z)$의 값이 $p(z|x)$와 비슷하다면 우리는 $q(z)$를 통해 사후확률을 계산하면 되는 것이다.  $q(z)$는 $\phi$라는 파라미터로 매개변수화 되고, 이를 variational paratemeter라고 한다. 따라서 VI의 목적은 $q(z|\phi)$가 $p(z|x)$와 가깝도록 하는 어떤 파라미터 $\hat \phi$를 찾는다. 그리고 실제 사후확률에 대한 근사값 $q(z|\hat \phi)$을 반환한다. 

  Variational Inference는 $q(z)$와 $p(z|x)$의 가까운 정도를 측정하기 위해 KL 다이버전스를 이용한다. 이는 위에서 살펴보았던 evidence와 ELBO 값의 차이로 정의된다.  

$$ KL( q(z) || p(z|x)) := \mathbb E_{Z \sim q(Z)} \bigg [\log{ q( Z) \over p(Z|x)} \bigg] $$

 VI는 KL 다이버전스를 최소화하는 분포를 찾는다. 이는 아래와 같이 표현할 수 있다. 

$$ \hat q := \arg \min_q KL(q_\phi (z) || p(z|x)) $$

$$ \hat \phi = \arg \min_ \phi KL(q_\phi (z) || p(z|x)) $$

 

  위 문제의 해는 $q(z)$와 $p(z|x)$에 대한 KL 다이버전스를 최소화하는 해이다. 그런데 문제는 여전히 KL 다이버전스 값을 우리는 계산할 수 없다는 것이다. $p(z|x)$를 계산하려면 $p(x, z) \over p(x)$를 계산해야하기 때문이다.  대신에 우리는 우회해서 우변을 최소화한다. KL 다이버전스(좌변)는 evidence와 ELBO 값의 차이(우변)로 정의된다는 것이었다. 이는 곧 KL 다이버전스를 최소화하는 문제는 evidence와 ELBO 값의 차이를 최소화하는 문제이며 evidence는  q에 의존하지 않기 때문에 ELBO를 최대화하는 것과 동일하다! 그래서 우리는 베이지안 추론을 근사하는 문제를 최적화 문제로 바꿀 수 있는 것이다. (evidence가 q에 의존하지 않는다는 것은 최적화 과정에서 미분에 의해 사라질 것이라는 것음 암시한다.)

 

Calculation

우변의 evidence 값을 최소화하면서 ELBO를 최대화하면 KL 다이버전스의 값을 0으로 만들 수 있을 것이다. 이제 이 계산을 어떻게 직접하는지 알아보자. KL 다이버전스의 값은 $p(z|x)$ 항을 계산할 수 없어서 여전히 KL 값을 얻기 어렵다. KL 다이버전스의 식을 다시 정리해보자. $p(z|x)$에 베이즈룰을 적용할 것이다. 아래 식에서 $q_\phi(z)$에 대한 파라미터 $\phi$는 생략 했다. 

$$\begin{align} KL(q (z) || p(z|x)) &= \int q(z)\log {q(z) \over p(z|x)}dz  \\ &= \int q(z)\log {q(z)p(x) \over p(x|z)p(z)}dz \\ &= \int q(z) \bigg ( \log q(z) + \log p(x) - \log p(x|z) - \log p(z) \bigg ) dz \\ &= \int q(z) \bigg ( \log{q(z)\over p(z)} + \log p(x) - \log p(x|z) \bigg ) dz  \\ &= \mathbb E_q \bigg [\log {q(z)\over p(z)} \bigg ] + \mathbb E_q [\log p(x)] - \mathbb E_q[\log p(x|Z)] \\ &=  \mathbb E_q [\log p(x)]  + \mathbb E_q \bigg [\log {q(z)\over p(z)} \bigg ] - \mathbb E_q[\log p(x|Z)] \\ &=  \mathbb E_q [\log p(x)]  - \bigg ( \mathbb E_q[\log p(x|Z)] - \mathbb E_q \bigg [\log {q(z)\over p(z)} \bigg ]\bigg ) \\ &= \mathbb E_q [\log p(x)] - \mathbb E_{Z \sim q(Z)} \bigg [ \log {p(x, Z) \over q(Z) } \bigg ] \\ &= \text {evidence} - \text {ELBO}  \end{align}$$

위에서 살펴보았던 evidence - ELBO 라는 식이 그대로 나온다. gradient descest 같은 최적화 방법을 이용해서 q를 학습시키면 evidence 값은 미분에 의해 사라진다. 결국 ELBO만을 최대화하면 되니까 우리는 다음의 식을 최대화하게 된다. 

$$\begin{align} \text {ELBO} &= \mathbb E_{Z \sim q(Z)} \bigg [ \log {p(x, Z) \over q(Z) } \bigg ] \\ &= \mathbb E_{Z \sim q(Z)} \bigg [ \log {p(x|Z)p(Z) \over q(Z) } \bigg ] \\ &= \mathbb E_{Z \sim q(Z)} \bigg [ \log {p(x|Z) + \log p(Z) - \log q(Z) } \bigg ] \end{align}$$

 

뉴럴 네트워크 학습의 관점에서 봤을 때 위 식을 loss로 설정하고 위 식을 최소화하는 방향으로 파라미터 $\phi$를 학습시키면 최대화 문제를 풀 수 있게 된다. 

6. Monte Carlo ELBO

우리는 실제 사후확률에 대한 분포를 모르므로 $q_\phi (z)$로부터 데이터를 샘플링해서 기댓값을 구할 것이다. 그런데 문제가 있다. $z$를 샘플링해서 값을 사용하게 되면 계산 그래프 과정에서 연결이 끊어져서 역전파를 할 수 없게 된다. 즉, 샘플링 과정은 미분 불가능하다. 
$$ z \sim q(\mu, \sigma^2)$$

Reparameterization trick

 위처럼 $z$를 $q(z)$로부터 직접 샘플링 하는 대신, reparameterization trick을 사용한다. $z$ 샘플을 $mu$와 noise의 합으로 표현하는 것이다. 
$$z = \mu + \sigma \circ \epsilon, \ \text {where} \ \epsilon \sim \cal {N}(0, 1)$$

코드를 구현하면 아래와 같이 구현된다. negative elbo를 계산하는 함수를 보면 elbo 계산식이 그대로 사용되는 것을 확인할 수 있다. 

 

class VariationalDistribution(nn.Module):
    def __init__(self, input_dim, latent_dim, output_dim):
        super(VariationalDistribution, self).__init__()
        self.latent_dim = latent_dim
        self.fc1 = nn.Linear(input_dim, latent_dim)
        self.fc2 = nn.Linear(latent_dim, latent_dim)
        self.fc3 = nn.Linear(latent_dim, latent_dim)

        self.q_mean = nn.Linear(latent_dim, output_dim)
        self.q_log_var = nn.Linear(latent_dim, output_dim)

    def reparameterize(self, mu, log_var):
        sigma = torch.exp(0.5 * log_var) + 1e-5
        eps = torch.randn_like(sigma)
        return mu + sigma * eps
    
    def forward(self, x):
        x = F.leaky_relu(self.fc1(x))
        x = F.leaky_relu(self.fc2(x))
        x = F.leaky_relu(self.fc3(x))
        
        mu = self.q_mean(x)
        log_var = self.q_log_var(x)
        log_var = torch.clamp(log_var, min=1e-5)
        return self.reparameterize(mu, log_var), mu, log_var
        
 def log_liklihood_gaussian(y, mu, log_var):
    sigma = torch.exp(0.5 * log_var)
    return -0.5 * torch.log(2* np.pi * sigma**2) - (1 / (2 * sigma ** 2) * (y-mu)**2)

def calculate_negative_elbo(y_pred, y, mu, log_var):
    # liklihood 
    likelihood = log_liklihood_gaussian(y, mu, log_var)
    
    # prior
    log_prior = log_liklihood_gaussian(y_pred, 0, torch.log(torch.tensor(1.0)))

    # q_prob: variational dist of y_pred
    log_q_prob = log_liklihood_gaussian(y_pred, mu, log_var)
    
    elbo = (likelihood + log_prior - log_q_prob).mean()
    return -elbo

References

[1] https://ko.wikipedia.org/wiki/%EB%B2%A0%EC%9D%B4%EC%A6%88_%EC%B6%94%EB%A1%A0

[2] https://stats.stackexchange.com/questions/243746/what-is-probabilistic-inference

[3] https://datascienceschool.net/03%20machine%20learning/17.02%20%EA%B7%B8%EB%9E%98%ED%94%84%20%ED%99%95%EB%A5%A0%EB%AA%A8%ED%98%95.html

[4] https://fabiandablander.com/r/Variational-Inference.html

[5] http://norman3.github.io/prml/docs/chapter04/4.html

[6] https://towardsdatascience.com/variational-bayes-4abdd9eb5c12

[7] https://en.wikipedia.org/wiki/Variational_Bayesian_methods

[8] https://mbernste.github.io/posts/elbo/

[9] https://mbernste.github.io/posts/variational_inference/

[10] https://www.ritchievink.com/blog/2019/09/16/variational-inference-from-scratch/